Neste artigo, vamos falar sobre o controle PID e como utilizar-lo em aplicações que exigem um controle mais preciso. Inicialmente, você vai entender o significado das letras PID (Proportional, Integral, Derivativo) E para explicar vamos iniciar com um exemplo bem simples para melhor compreensão.
Posteriormente, iremos adentrar um pouco mais a fundo no significado de cada um dos termos do PID e no final, faremos um exemplo prático para memorizarmos os conceitos aqui colocados.
Vamos supor que você está dirigindo pela estrada e tentando manter uma distância definida atrás do carro que está na sua frente, mensurada aqui como distância X.
1 – P é para Proporcional
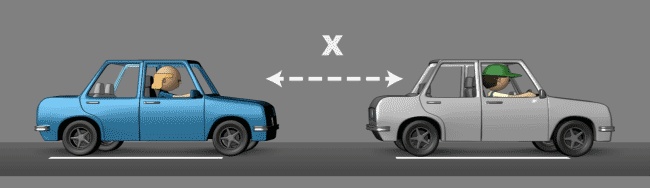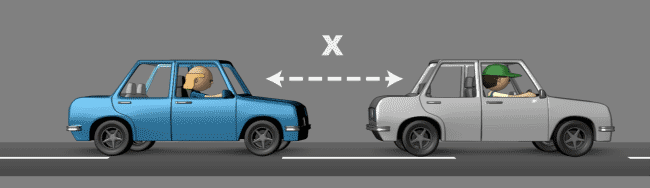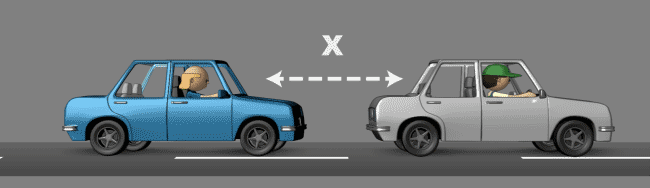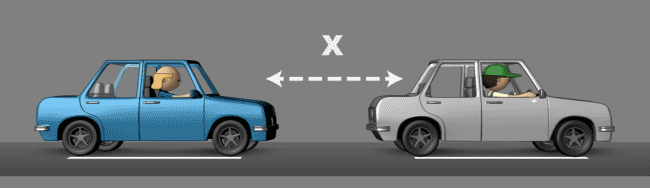
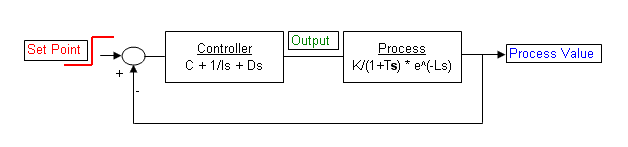
Figura 1 – Controle PID – Proporcional
Se você está seguindo um carro a uma distância X e você começa a ficar mais longe dele, então deverá acelerar proporcionalmente para retornar novamente ao ponto X.
No entanto, se você acelerar muito vai acabar passando do ponto X, tornando a distância agora menor do que X e neste caso deverá frear para não bater no carro da frente e voltar ao ponto X.
Mas se você frear e desacelerar muito, vai passar X novamente e terá de acelerar novamente para voltar ao X. Isso continuará se repetindo caso a sua aceleração proporcional não for a correta.
A aceleração que é impressa ao pisar no acelerador para ganhar velocidade e alcançar o veículo é chamada de ganho ou proporcional em um controle PID. Veja que se o ganho for alto, acabamos por passar do ponto alvo (Setpoint) e então devemos imprimir uma correção. Por este motivo é comum ver uma oscilação (acima e abaixo do Setpoint) quando não temos um ganho bem definido.
2 – I é lntegral
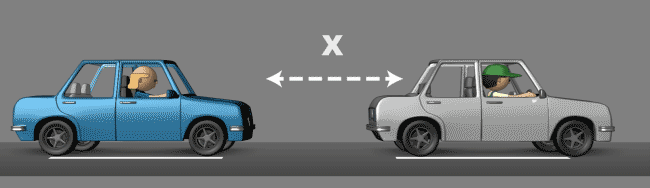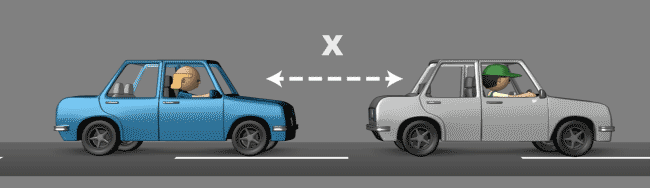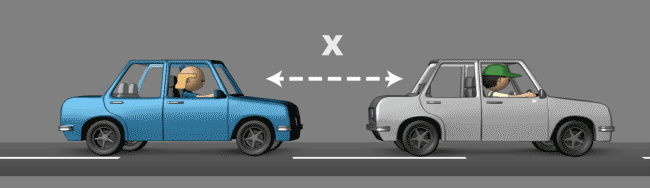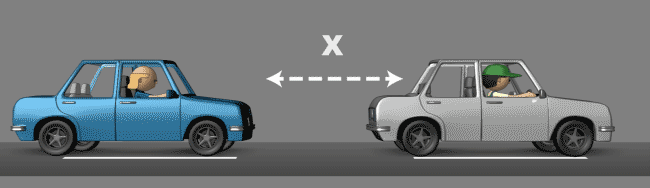
Figura 2 – Controle PID – Integral
A integral ajuda você a recuperar a distância X novamente e mantê-la de forma precisa. O integral em nosso exemplo, seria você estar a uma distância maior que X do veículo da frente e pisar levemente no acelerador alcançando exatamente à distância X e mantendo-a muito mais suave do que apenas proporcionalmente (acelerando e desacelerando). Este procedimento pode ser comparado ao tempo integral de um controle PID.
3 – D é Derivativo
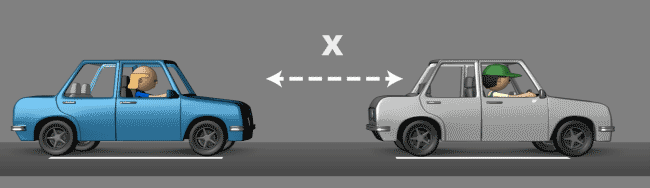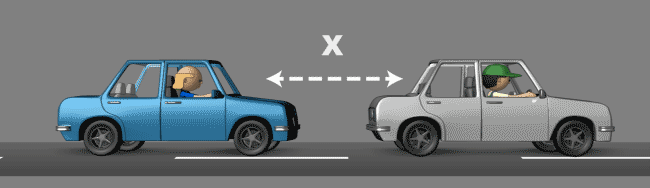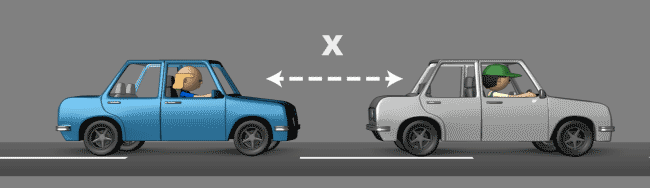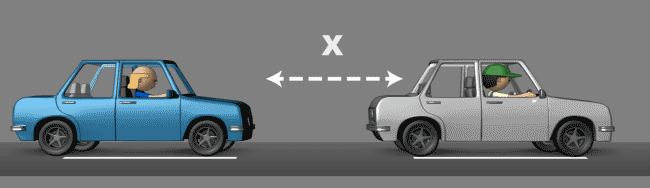
Figura 3 – Controle PID – Derivativo
No controle PID, a derivada é usada para eliminar um erro acumulado na integral. Em nosso exemplo isso seria você perceber a distância X crescer ou decrescer e rapidamente, impedir que esta diferença fique maior. O derivativo age para diminuir a oscilação em torno do Setpoint tornando-a o menor possível.
Você Gostou Deste Artigo?
Cadastre-se hoje e receba atualizações por e-mail. Respeitamos a sua privacidade e você nunca terá seu e-mail divulgado.
4 – O Exemplo do Veículo a uma Velocidade Desejada
Outra forma de entender o controle PID é ao invés de imaginarmos a distância entre dois carros, imaginarmos a situação do carro que vai viajar a uma velocidade constante:
Se o carro estiver parado e ao sair quisermos atingir uma velocidade de 80 km/h, podemos pressionar o pedal do acelerador de forma que a velocidade do veículo aumente a uma velocidade próxima do objetivo de 80 km/h que poderia ser de 75 km/h.
Quando chegamos nos 75km/h, começamos a aliviar o pedal do acelerador para evitar que o veículo vá além dos 80km/h. Este alívio no pedal do acelerador pode ser diretamente comparado com a entrada da banda proporcional ou da banda em relação à velocidade requerida.
Veja que se não olharmos para o velocímetro, certamente conduziremos o carro a uma velocidade que não é a nossa velocidade desejada e teremos um erro (para cima ou para baixo). O PID aqui é o proporcional.
Se olharmos agora para o velocímetro e observarmos que estamos abaixo da nossa velocidade desejada (no caso a 75 km/h), podemos usar esse feedback visual para corrigir o erro (que no caso é de -5 km/h) e começar a pressionar lentamente o pedal do acelerador.
Como resultado, nossa velocidade aumenta lentamente, diminuindo o erro e atingindo a velocidade desejada de 80 km/h (Setpoint). Este é o integral entrando em ação.
Agora estamos exatamente em nosso Setpoint de 80 km/h, e continuamos a manter essa velocidade através do feedback visual do velocímetro. Mas se nos deparamos com uma mudança repentina na inclinação da estrada, como uma colina íngreme, temos que corrigir a redução de velocidade por conta da subida pressionando o pedal do acelerador mais do que seria necessário em uma reta.
Se após subir a colina e encontrarmos novamente uma reta, é necessário desacelerar um pouco para evitar que a velocidade ultrapasse os 80km/h e fique constante no Setpoint desejado.
A quantidade de correção e o tempo para estabilizar o erro (diferença da velocidade em torno do Setpoint) para zero pode ser comparado ao derivativo no controle PID. Por isso falamos que o derivativo trata diretamente da oscilação em torno do objetivo.

Figura 4 – Termos do controle PID para a velocidade de um veículo
Vamos agora pegar o exemplo de estabelecer uma velocidade ao veículo em que nós somos o condutor e, portanto, o controlador do processo de mudar a velocidade do carro e criar o diagrama de blocos de controle para tal. Veja abaixo na Figura 5 em que representamos o loop de controle do carro andando a uma velocidade constante.
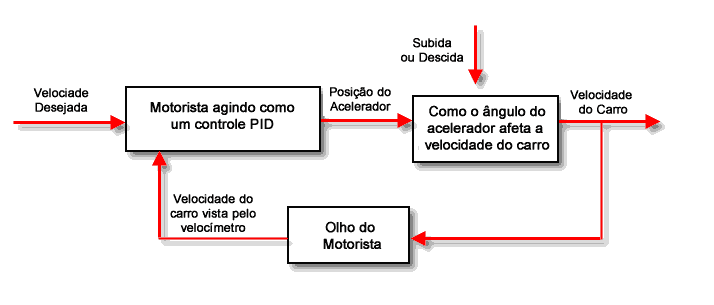
Figura 5 – Diagrama de blocos de controle para velocidade de um carro
Observe pela Figura 5 como é importante fechar o loop de realimentação. Veja que se removermos o loop do feedback (olho do motorista no velocímetro), estaremos entrando em “controle de loop aberto” e neste caso teremos que controlar a posição do carro com os olhos fechados!
Isso obviamente é impossível, mas felizmente estamos sob “controle de loop fechado” utilizando nossos olhos para o feedback de posição.
A maioria dos sistemas de controle funcional de trabalham de forma análoga ao exemplo acima. Assim, em um sistema de controle de temperatura industrial por exemplo, o controlador de temperatura toma os sinais PV (valor real que pode ser coletado por um sensor de temperatura termopar) e SP (Setpoint ou valor desejado inserido diretamente no controlador) e então coloca estes sinais em uma caixa preta que calcula qual deve ser a saída do controlador.
Essa saída do controlador é enviada então para um atuador que se move para realmente controlar o processo. O atuador poderia ser um drive que dosa a energia na resistência que por sua vez aquece um forno industrial.
Estamos interessados aqui no que esta caixa preta realmente faz e quais são os cálculos proporcional, integral e derivativo que a partir da medição do valor PV, são aplicados de forma com que o sistema atue para que o valor chegue no Setpoint. Estes cálculos, chamados de “Modos de Controle” que incluem:
- Proporcional (P)
- Integral (I)
- Derivativo (D)
Para evoluir no nosso entendimento, vamos ver abaixo uma forma simplificada de como o controle PID atua em um sistema de controle de temperatura. Veja que o diagrama de blocos neste caso é exatamente o da Figura 5 que utilizamos para representar a velocidade do veículo. No entanto, detalhamos um pouco mais o bloco de controle PID.

Figura 6 – Diagrama de blocos para o controle de Temperatura
Veja que é realmente muito simples o conceito do controle PID. O PV é subtraído do SP para criar o erro. O erro é simplesmente multiplicado por um, dois ou todos os termos P, I e D calculados (dependendo de quais são ativados). Em seguida, as “ações de controle de erro x” resultantes são somadas e enviadas para a saída do controlador.
A saída do controlador por sua vez vai para um atuador característico do processo e do seu comportamento para obter a temperatura desejada. Esta nova “caixa preta” chamamos de Função de Transferência do Processo e como o nome diz, ela modela cada tipo de processo e se diferencia em termos de comportamento dependendo de cada aplicação.
Um pedal do acelerador por exemplo influencia na velocidade do carro e este comportamento é muito diferente do que a regulagem da fonte de energia na resistência de um forno. Por isto, a função de transferência do processo depende de cada aplicação.
Os modos P,I e D de controle PID podem ser usados em combinações diferentes conforme abaixo:
P – Às vezes utilizado;
PI – O mais utilizado na indústria e em diversas outras aplicações;
PID – Às vezes utilizado;
PD – Raramente utilizado, mas pode ser útil para controlar servomotores.
5 – Entendendo os Termos P, I e D e suas Combinações
5.1 – Derivativo
Entre na sala de controle de uma planta de processo e pergunte ao operador:
“Qual é o derivativo da pressão do reator 4?”
E a resposta será tipicamente:
“Não entendi a sua pergunta!”
No entanto se você entrar na sala e perguntar:
“Qual é a taxa de mudança da pressão do reator 4?”
Neste caso, o operador irá examinar o gráfico de tendência da pressão e dizer algo como:
“Cerca de 5 PSI a cada 10 minutos”
Para obter esta resposta o operador apenas olhou o gráfico de pressão e verificou que ela oscilou em 5PSI no período de 10 minutos. Assim, o derivado é apenas um termo matemático que significa taxa de mudança. Isso é tudo que há para ele.
5.2 – Integral
Não é de se admirar que tantas pessoas possuem medo do conceito de integrais e integração, quando nos deparamos com esta definição extraída do Wikipedia:

Figura 7 – Definição de integral Wikipedia
O que!?!? Se você entendeu sem nunca ter estudado cálculo, então é uma pessoa muito esperta. No entanto, ao resumir o conceito de integral, teremos:
O integral de um sinal é a soma de todos os valores instantâneos que o sinal possui, do início em que você começou a contar até que você parou de contar.
Portanto, se você possui um sinal com uma determinada tendência e este sinal é amostrado a cada segundo, e imaginando que ele seja a medição de uma temperatura. Neste caso, se você fosse sobrepor a integral do sinal nos primeiros 5 segundos obteria o seguinte:

Figura 8 – Gráfico do cálculo de integral
No gráfico, a linha verde é a temperatura, os círculos vermelhos são onde seu sistema de controle tem amostrado a temperatura e a área cinza é o integral do sinal da temperatura.
A integral é o somatório dos valores de 5 temperaturas durante o período de tempo em que você está interessado em integrar. Em termos numéricos é a soma das áreas de cada um dos retângulos cinzas:
Integral = (13 x 1) + (14 x 1) + (13 x 1) + (12 x 1) + (11 x 1) = 63° Cs
A unidade curiosa (Cs ou graus Celsius x segundos) é somente porque temos que multiplicar uma temperatura por um tempo, mas não se preocupe com isso pois neste as unidades não são importantes.
Como você provavelmente pode observar a integral acaba por ser a área sob a curva e quando temos sistemas do mundo real, nós realmente conseguimos obter uma aproximação para a área sob a curva utilizando o método mostrado no exemplo da Figura 8. Neste caso é mais simples de ver e entender e não precisamos realizar nenhum cálculo complexo..
5.3 – Controle Proporcional
Aqui está um diagrama do controlador quando habilitamos somente o controle P:
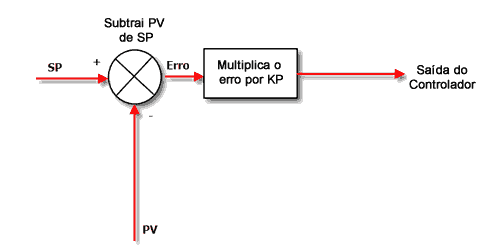
No modo Proporcional, o controlador simplesmente multiplica o Erro pelo Ganho Proporcional (Kp) para obter a saída do controlador. Veja que o Ganho Proporcional do PID, é o ajuste que sintonizamos para obter o desempenho desejado de um controlador “P somente”.
5.4 – O controlador P + I
Se colocarmos a ação proporcional e integral juntas, obteremos o controlador PI e o diagrama abaixo mostra como o algoritmo em um controlador PI é calculado.

O que fica complicado quando você aplica uma ação Integral no PID, é que esta ação realmente estragará seu processo a menos que você saiba exatamente o quanto de ação Integral deverá aplicar.
Uma boa técnica de ajuste PID pode te ajudar a saber exatamente o quanto de Integral se aplicará a um processo específico e veremos isso no final deste artigo. No entanto, como a ação integral pode ser ajustada em um primeiro momento?
5.5 – Ajustando a Ação Integral
Uma boa maneira de ajustar o quanto de ação Integral no PID você tem que ter, é ajustando um termo chamado “minutos por repetição”. Não é um nome muito intuitivo é? Então, de onde vem este estranho nome? Esta é uma medida de quanto tempo levará para que a ação Integral coincida com a ação Proporcional.
Em outras palavras, se a saída da caixa proporcional no diagrama acima for de 20%, o tempo de repetição é o tempo que levará para a saída da caixa Integral chegar a 20% também.
E o ponto importante a notar é que quanto maior for a ação integral, mais rápido ele vai ter esse valor de 20%. Ou seja, levará menos minutos para chegar lá e então o valor de “minutos por repetição” será menor.
Em outras palavras, quanto menor o “minutos por repetição”, maior a ação integral.
Para tornar as coisas um pouco mais intuitivas, muitos controladores usam uma unidade alternativa de “repetições por minuto”, que é obviamente o inverso de “minutos por repetição”. A coisa agradável sobre “repetições por minuto” é que quanto maior ela é, maior será a ação resultante da Integral.
5.6 – Ação Derivada – Prever o Futuro
Ok, então a combinação de ação P e I parece atender todas as aplicações e fazer um bom trabalho no que tange ao controle de sistemas. Essa é a razão pela qual os controladores PI são os mais populares pois eles fazem o trabalho bem o suficiente e ao mesmo tempo mantem as coisas simples.
Mas os engenheiros que são engenheiros estão sempre pensando em melhorar o desempenho e o desempenho máximo pode ser alcançado adicionando o ingrediente final no loop PID: a ação Derivativa.
Adicionando a ação derivativa pode permitir que você tenha maiores ganhos de P e I e ainda manter o loop estável, dando-lhe uma resposta mais rápida e melhor desempenho de loop.
Se você pensar nisso, a ação Derivativa pode melhorar a ação do controlador porque ela prediz o que ainda está por acontecer ao projetar a taxa atual de mudança para o futuro. Isto significa que não está sendo contabilizado o valor medido atual, mas sim um valor de medição futuro.
As unidades usadas para a ação derivada descrevem até que ponto você deseja olhar para o futuro. Exemplo: se a ação derivada for de 20 segundos, o termo derivativo projetará a taxa de variação atual para o futuro em 20 segundos.
O grande problema com o controle utilizando o D é que se você tem ruído em seu sinal (que se parece com um monte de picos com lados íngremes) isso sobrecarrega totalmente o algoritmo pois quando ele verifica a inclinação do pico de ruído. logo ele “pensa” que o processo está mudando rapidamente, sobrecarregando a ação D fazendo a sua saída de controle saltar por todo o lugar, estragando o controle.
Claro que você pode tentar filtrar o ruído, mas o meu conselho é que, a menos que o controle PI seja realmente lento, não se preocupe com a ação D.
6 – Um Exemplo Prático de Controle PID
Para este exemplo, a fim de descomplicar e ir direto ao ponto, utilizaremos uma planilha para o cálculo dos parâmetros de processo e de controle e que você pode baixar clicando no link abaixo:
Veja que na planilha temos 2 funções transferência (a do controlador e a do processo). Para o controlador, vamos ter que determinar os parâmetros Proporcional (C), Integral (Is) e Derivativo (Ds). Já para o processo seguimos a seguinte regra:
Uma função transferência de processo é caracterizada por 3 parâmetros:
- Ganho do Processo (K) – a relação entre a variação da variável de processo com relação entre a variação da variável manipulada;
- Constante de tempo (T) – mede a velocidade de resposta:
- Tempo morto (L) – tempo entre a movimentação da variável manipulada e o início da resposta do processo;
Uma das maneiras mais comuns de obter esses parâmetros é fazendo um teste passo a passo. Como falei anteriormente, tenha em mente que cada processo possui diferenças de parâmetros e o intuito aqui não é demonstrar como fazer este teste.
Apenas vamos considerar alguns parâmetros de processos comuns para realmente focar no que interessa que é o PID, pois na prática dificilmente você terá estes parâmetros e terá que testar o PID sem eles como faremos após esta etapa independentemente de qual processo for o seu.
Em um processo químico, os loops são frequentemente mais rápidos, com ganhos (K) variando de 1 a 10, constante de tempo (T) variando de alguns segundos a alguns minutos e alguns segundos de tempo morto (L).
Loops de temperatura por outro lado são geralmente muito mais lentos, com tempo morto e de resposta no intervalo de alguns minutos.
6.1 – Método Prático para Determinar os Parâmetros PID
Um método mais fácil de determinar manualmente os valores P, I e D é zerar os termos Integral e Derivativo setar um valor pequeno para o Proporcional a fim de obter a Banda Proporcional a um mínimo. A largura de oscilação resultante Xosc e o período de oscilação Tosc podem então ser usados para determinar as configurações de PID utilizando as fórmulas abaixo:
- P = 2,0 * Xosc
- I = 1.5 * tosc
- D = I / 5
Os valores obtidos com as fórmulas acima resultam em uma resposta ligeiramente mais amortecida e consequentemente todos os valores podem ser reduzidos ligeiramente para dar um Loop mais responsivo.
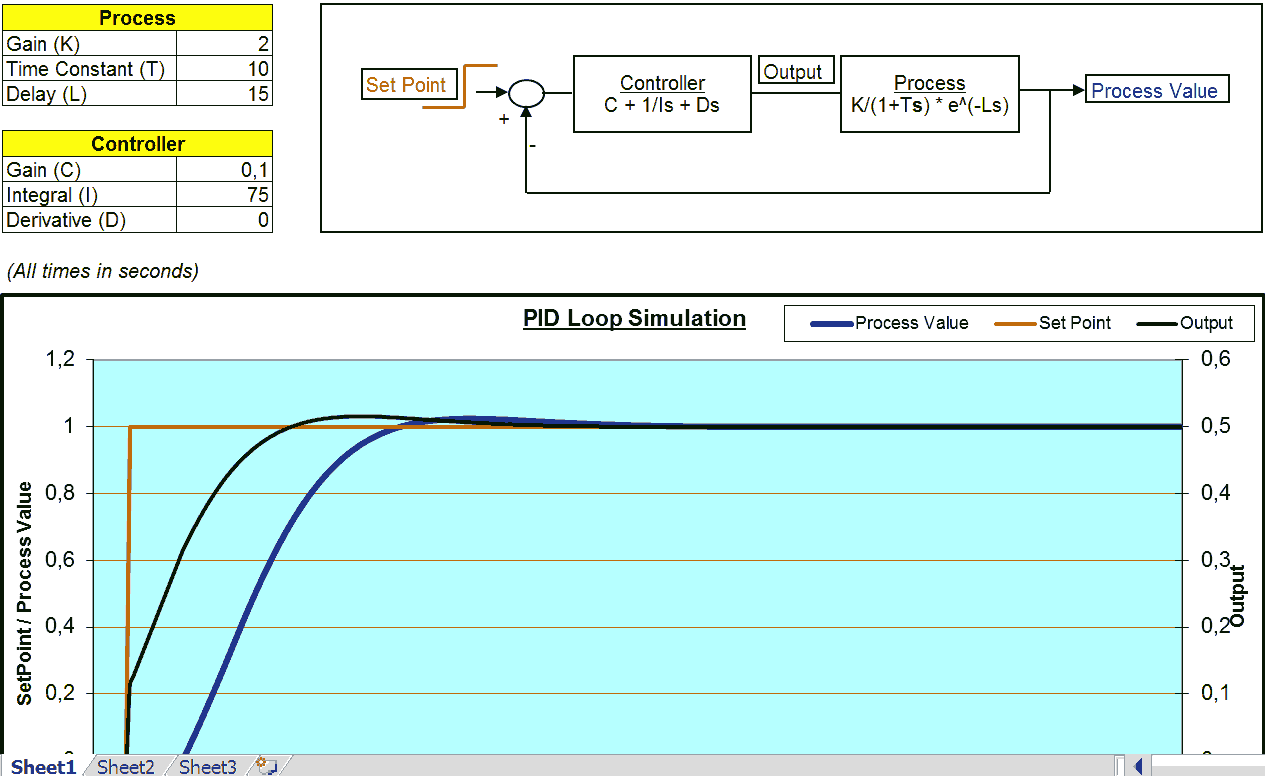
No exemplo então, utilizei os valores de processo (K=2, T=10 e L=15) e zerei os termos I e D. Após isso, fui chutando um valor pequeno de C (0,1 ; 0,2: 0,3, etc….). Em 0,3 você pode perceber que já conseguimos ter uma pequena oscilação para analisar. Assim, consegui obter um valor próximo para a amplitude e período.
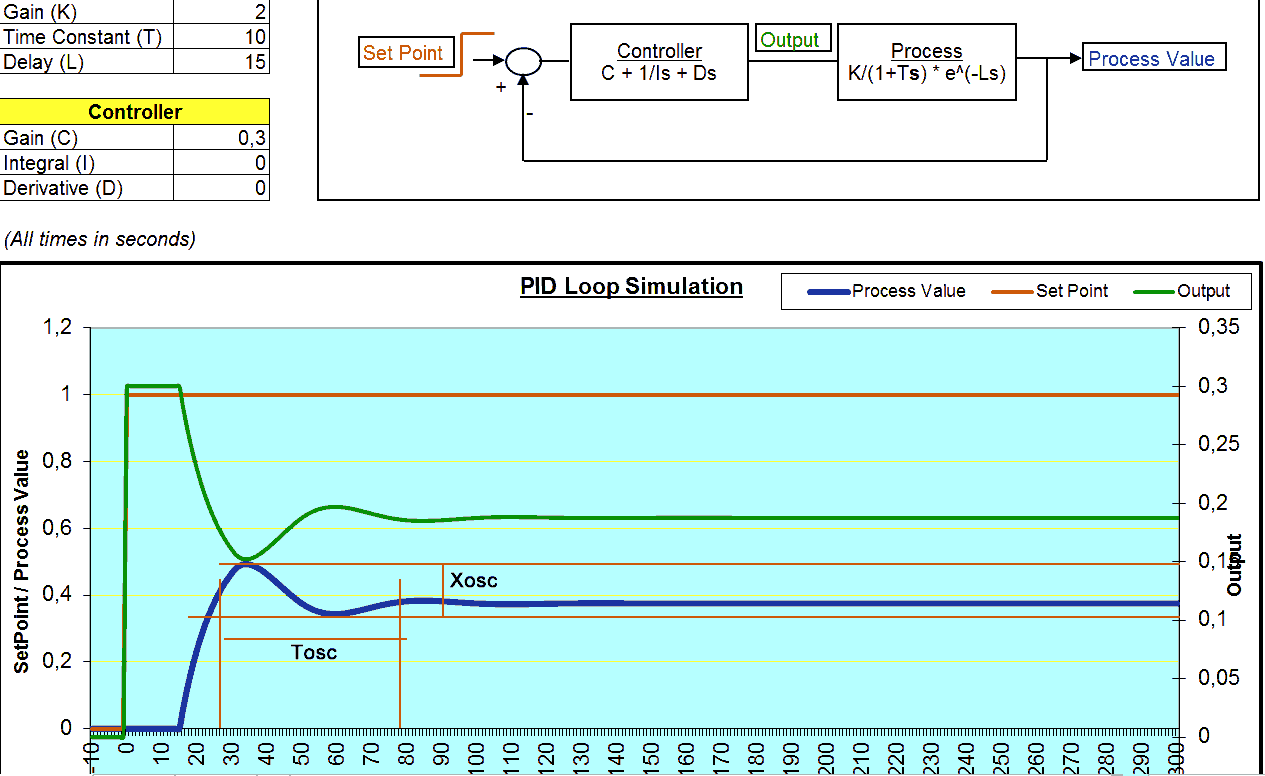
Abaixo, estão os valores obtidos a partir da análise do gráfico (Xosc e Tosc) e os valores calculados (P e I):
- Xosc = 0,05
- Tosc = 50
- P = 2*Xosc = 0,1
- I = 1,5*50 = 75
Com os valores obtidos, então agora podemos ajustar o C e o I. Veja que o resultado foi um controle muito próximo do que precisamos e como na maioria dos casos, nem precisamos utilizar o D.
Para finalizar, deixo aqui um vídeo com exemplo prático de um controle PID
Referências: