Confiabilidade e disponibilidade de máquinas: um exemplo prático

Formula da função de  Weibull

Onde:

• F(t) é a probabilidade de falha para uma determinada amostra;
• t é o tempo até a falha;
• η é a característica de vida ou parâmetro de escala;
• β é o parâmetro de inclinação ou forma

A análise de Weibull é um método de modelagem de dados conjuntos contendo valores maiores que zero (como exemplo, podem ser dados de tempo até a falha conhecido como time-to-fail (TTF)). Uma característica importante desta análise, é que se houver a possibilidade de fazer uma coleta de 3 amostras, já é viável realizar o estudo de confiabilidade. Através da utilização de Weibull, é possível responder alguns problemas de engenharia tais como:

• Um operador reporta três falhas de um mesmo componente funcionando pelo período de três meses. O gerente da área questiona: “quantas falhas teremos no próximo trimeste, semestre ou ano? Quanto vai custar? Qual é a melhor ação corretiva para reduzir os riscos e as perdas?
• Para adquirir peças de reposição e agendar o trabalho da equipe de manutenção, quantos componentes serão enviados para revisão mês a mês no próximo ano, sabendo-se que o gerente de manutenção quer ter 95% de certeza de que as peças em estoque e a mão-de-obra serão o suficientes?
• O custo de uma falha não prevista de um componente (manutenção corretiva) é em torno de 20 vezes o custo de uma manutenção planejada. Qual é o intervalo ideal (melhor custo-benefício) que deve ser estabelecido para a substituição deste componente?

2 – Exemplo prático do cálculo de confiabilidade envolvendo disponibilidade

O efeito de testes e atividades de manutenção realizados em um componente baseia-se em duas situações extremas. A primeira delas supõe que o estado do componente após a manutenção é “tão bom como novo”, o que significa que sua idade é restaurada para zero depois que uma atividade de manutenção é executada. A segunta opção assume que a manutenção deixa o componente em uma condição “tão ruim quanto velho”, significando que sua idade é a mesma depois de realizada a manutenção se comparada com a situação imediatamente antes da manutenção. No nosso exemplo de confiabilidade nos basearemos na primeira opção, ou seja, a de que após a manutenção o componente terá sua idade restaurada. Para realizar os cálculos dos parâmetros, será utilizado o Excel 2010 e o módulo de ferramenta de análise deste software.

Para o exemplo, vamos considerar um cilindro hidráulico que de tempos em tempos, devido ao desgaste das gaxetas e anéis de vedação, falha com relação à sua função principal, exigindo manutenção corretiva. Será então calculado o melhor momento para realizar a manutenção periódica a partir da análise dos custos e da confiabilidade.

Com relação ao cálculo da confiabilidade, primeiramente é necessário que tenhamos em mãos a amostragem de tempo até a falha do cilindro. Sendo assim, foi coletado em campo o tempo em minutos que o cilindro operou antes de cada falha, conforme a Figura 1 abaixo:

Figura 1- Valores de tempo até a falha do cilindro hidráulico

Pelos valores podemos perceber que em média a cada 4 meses e 26 dias (210379 minutos), ocorre a falha do cilindro, exigindo manutenção corretiva. Aqui foi coletado um total de 10 amostras, porém, a partir de 3 amostragens já é possível realizar o estudo de confiabilidade.

Com os dados de amostragem de tempo até a falha, vamos agora calcular as variáveis necessárias para obter os parâmetros da fórmula de Weibull (beta e alfa). Não é o intuito deste artigo ir a fundo na estatística e mostrar o porquê das fórmulas e sim como utilizar a ferramenta. Sendo assim, voltemos ao exemplo:

A partir dos dados de tempo até a falha, deve-se preencher outra tabela conforme indicado na Figura 2 abaixo. Os passos são o seguinte:

1. Na coluna A, deve-se preencher os dados até a falha e logo após ordenar eles por ordem do menor para o maior. Feito isto, deve-se proceder ao passo2;
2. Na coluna B, deve-se numerar em sequência de acordo com a quantidade de amostras;
3. Para preencher a coluna C, é necessário calcular o Median Rank. É um conceito da estatística que pode ser calculado da seguinte forma: Na célula C15 digite a fórmula “=(B15-0,3)/(10+0,4)”. Os valores 0,3 e 0,4 são padrões na obtenção do median rank. Já o valor “10” foi utilizado porque representa a quantidade de amostras. Feito isto extenda a fórmula para as outras células, conforme indicado na tabela2.
4. A coluna D deve conter os valores obtidos através da fórmula “1/(1-Median Rank)”.
5. Da mesma forma a coluna E deve conter valores obtidos através da fórmula “Ln(Ln(1/(1-Median Rank)))”, onde Ln é o logaritmo do valor.
6. Finalmente na coluna F deve ser calculado o logaritmo do ttf (coluna A), utilizando a fórmula “Ln(TTF do Cilindro)”.

A tabela completa com os valores calculados pode ser visualizada abaixo (Tabela 2).

Figura 2 – Valores calculados para análise confiabilidade

Com a tabela completa, agora é necessário utilizar o recurso de regressão do Excel, que faz parte da ferramenta Análise de dados. Deve-se proceder da seguinte forma:

1. Clicar na opção Análise de Dados, localizada no menu Dados. Caso o seu Excel não possua esta opção visível, é necessário habilitá-la. Para saber como fazer isto vá até o Item7 – Anexo deste artigo clicando aqui.
2. Clicar em Regressão.
3. Clicar Ok.

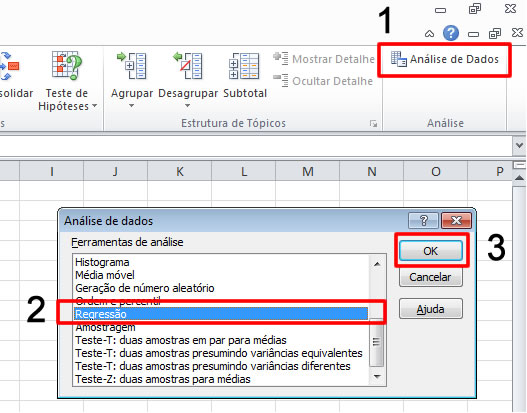
Figura 3 – Regressao linear no Excel

Agora, é necessário informar ao Excel quais serão as colunas utilizadas para a regressão. Assim, proceda da seguinte forma:

1. O intervalo Y de Entrada deve ser os dados da coluna E, incluindo o cabeçalho. Portanto é o intervalo compreendido entre o E14 e E24;
2. O intervalo X de Entrada deve ser os dados da coluna F, incluindo o cabeçalho. Portanto é o intervalo compreendido entre o F14 e F24;
3. Checar a opção Rótulos.
4. Checar a opção nova planilha e dar o seguinte nome: “Regressão Linear” ou qualquer outro nome que desejar.
5. Checar a opção “Plotar ajuste de Linha”.
6. Clicar no botão “Ok”.

Todos estes passos podem ser visualizados na Figura 4 abaixo:

Figura 4 – Configurar análise de regressao linear no Excel

O Excel automaticamente irá gerar uma planilha com os dados estatísticos calculados, bem como o gráfico de regressão. Porém, não temos ainda todos os dados necessários. É preciso ainda calcular os parâmetros beta e alfa através do seguinte procedimento:

1 – Na célula A19, digite: “beta (ou parâmetro de forma)”. Na célula B19, digite a fórmula: “=B18. Na célula A20, digite: “alfa (ou característica de vida)”. Na célula B20, digite a fórmula: “=EXP(-B17/B18). O resultado pode ser visualizado na Figura 5. Para este exemplo, temos então o  beta=4,2524 e o alfa=231126,77.

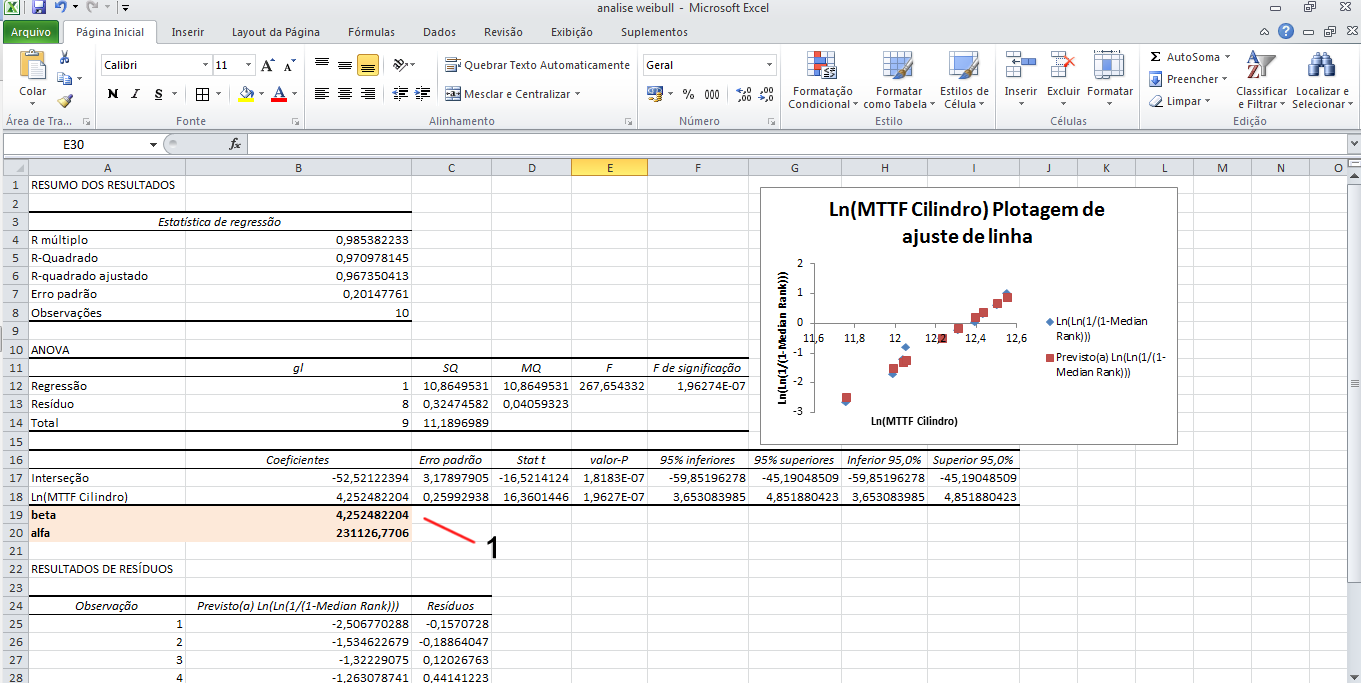
Figura 5 – Análise de regressão linear no Excel

O que representam os parâmetros β e α?

O parâmetro de forma β indica se a taxa de falha está crescente, constante ou decrescente. Se β<1, é um indicativo de que o produto está com a taxa de falha decrescente. Este cenário é típico da chamada “mortalidade infantil”, indicando que o produto falha logo no seu período de “nascimento”. Se β=1, é um indicativo de falha constante. São componentes que após sobreviverem ao “nascimento” possuem uma taxa de falha constante. Se β>1, temos então a situação de uma taxa de falha crescente. Este cenário é típico de produtos que falham por desgaste como é o nosso caso (β=4,25) em que o beta é muito maior do que 1, indicando que o cilindro falha por fadiga após um determinado tempo.

A característica de vida, ou parâmetro α é uma medida de escala ou propagação com relação à distribuição dos dados. Ele representa o número na escala do eixo X em que 63,2% dos cilindros falharam. Fazendo a análise de confiabilidade para nosso exemplo em que α=231.126, significa dizermos que 37% dos cilindros sobrevivem após um período de  231.126 minutos, ou melhor dizendo, após 5 meses e 11 dias.

3 – Como calcular os custos de manutenção Preventiva e manutenção Corretiva?

Custos de Manutenção Corretiva

No nosso estudo de confiabilidade, para o cálculo dos custos de manutenção corretiva, devem ser considerados, além do material e da mão-de-obra envolvida na atividade de reparo do componente, o custo das perdas causadas pelo lucro cessante.

Na prática, o lucro cessante pode ser calculado levando-se em consideração o tempo em que determinado equipamento ou máquina deveria estar produzindo e não produziu. É exatamente o que ocorre quando há a quebra ou falha de um componente da máquina que faz com que ela fique inoperante. Sendo assim, o lucro cessante é determinado quando é computado o lucro que a empresa deixou de ganhar durante o tempo em que a máquina ficou parada. Utilizando este conceito, vamos calcular os custos de manutenção corretiva para o exemplo do cilindro hidráulico.

No caso do cilindro hidráulico, ao analisar as falhas, foi cosntatado que quando ocorre a mesma, a máquina fica inoperante e sem produzir por um período em média de 4 horas. Isto ocorre devido à localização do cilindro na máquina e dificuldade de acesso. Este tempo de reparo abrange desde a parada da máquina, retirada do cilindro, troca do kit de vedação e gaxetas, recolocação na máquina e início de operação. Verificou-se também que para a manutenção corretiva, são utilizados 2 colaboradores com o custo da hora de R$13,00 cada um. Além disto, o kit de reparo de vedação e gaxetas custa R$ 300,00. A máquina do nosso exemplo produz perfilados e durante estas 4 horas em que a máquina ficou parada, ela deixou de produzir  480 perfilados. Sabe-se que cada perfilado tem o peso de 1 quilo e que o lucro por quilo produzido é de R$4,00. Vamos então calcular o custo de manutenção corretiva para este caso:

• Custo de mão-de-obra = qtd de colaboradores x tempo de reparo x custo da hora do colaborador = 2 x 4 x 13 = R$ 104,00;
• Custo de material = custo do kit de reparo = R$ 300,00;
• Custo de perda por lucro cessante = qtd de produto deixado de produzir no período x lucro unitário do produto = 480 x 4 = R$ 1.920,00.

Com estas três variáveis temos então o custo de manutenção corretiva (Cmc), que é calculado da seguinte forma:

Cmc = Custo de mão-de-obra + Custo de material + Custo de perda por lucro cessante

Cmc = 104 + 300 + 1920 = R$ 2.324,00

Custos de Manutenção Preventiva

A manutenção preventiva é uma manutenção que pode ser programada antes de ser realizada. Como isto geralmente é realizado em conjunto com a operação, a empresa não considera este tempo para o planejamento da produção e por este motivo não ocorre a perda por lucro cessante. Sendo assim, no cálculo do custo deverá ter somente o custo de mão-de-obra e o custo de material. Portanto o custo de manutenção preventiva (Cmp) será:

• Custo de mão-de-obra = qtd de colaboradores x tempo de reparo x custo da hora do colaborador = 2 x 4 x 13 = R$ 104,00;
• Custo de material = custo do kit de reparo = R$ 300,00.

Neste exemplo, consideramos o tempo de reparo da manutenção preventiva sendo exatamente o mesmo tempo gasto quando ocorre a manutenção corretiva, mas na prática este tempo tende a ser bem menor, justamente pelo fato da manutenção ser programada. Com o planejamento da atividade, o manutentor terá a disponibilidade imediata do material correto no momento da substituição (não haverá o tempo perdido de atender ao chamado da operação, deslocar até a máquina, verificar o que ocorreu, buscar o material no almoxarifado ou o risco de requisitar o material errado).

4 – Como calcular o ponto ótimo de manutenção baseando-se na confiabilidade e nos custos?

Custo total de manutenção e confiabilidade

Até agora, calculamos os custos de manutenção levando em consideração o momento em que elas ocorrem, não analisando o custo com o passar do tempo. No entanto, para definir a melhor estratégia de manutenção, é necessário que seja levado em consideração a probabilidade de falha do componente e sua confiabilidade ao longo do tempo. Somente desta forma, o custo poderá ser analisado fielmente como ocorre na realidade. Por exemplo, se após 3 meses, a probabilidade de um item sofrer manutenção corretiva for de 50% e o custo envolvido nesta manutenção for R$ 2000,00, é correto prever nos custos da empresa que em três meses irá incorrer uma despesa de manutenção corretiva com este item no valor de R$1.000. Este resultado é o valor de manutenção multiplicado pela probabilidade de falha, ou seja:

• Cmc (3 meses) = Cmc x probabilidade de falha nos 3 meses
• Cmc = 2000 x 0,5 = R$ 1.000,00

Devido aos motivos explicados acima, começa a ficar claro o porque de utilizar a análise de Weibull atrelada aos custos para fechar o estudo da confiabilidade. Isto porquea análise de Weibull representa exatamente a probabilidade de falha do componente ao longo do tempo.

Voltando ao exemplo do cilindro hidráulico, quando foram feitas as análises de regressão sobre a amostragem de tempo até a falha, obtivemos os parâmetros beta=4,2524 e alfa=231126,77 necessários para calcular as funções de confiabilidade e probabilidade de falha. Vamos agora desenhar estas curvas com a ajuda do Excel:

Na mesma pasta de trabalho anterior, crie uma nova planilha e insira os parâmetros alfa e beta conforme o procedimento:

1. Inserir os valores alfa e beta nas células B3 e B2 respectivamente;
2. Inserir um intervalo de tempo até a falha na coluna D que corresponda a amostragem. Neste exemplo, foi inserido 10 intervalos de tempo com espaçamento de tempo de 40.000 até atingir 400.000, pois o máximo de tempo até a falha atingido na amostragem que está sendo analisada foi de 300.000.
3. Calcular a função F(t), utilizando a seguinte fórmula: Na célula E2, digitar: “=WEIBULL(D2;$B$2;$B$3;VERDADEIRO)”. Feito isto, estender a fórmula para as outras células.
4. Calcular a função confiabilidade R(t) utilizando a seguinte fórmula: Na célula F2, digitar: “=(1-E2)”. Isto porque a função confiabilidade é o complemento da função probabilidade. Finalizando a fórmula, estender a fórmula para as outros células.
5. Inserir os custos de manutenção corretiva e manutenção preventiva do cilindro nas células B5 e B6, conforme Figura 6 abaixo:

Figura 6 – Funções de confiabilidade e probabilidade de falha.

Agora que temos as funções calculadas é possível obter os gráficos de probabilidade de falha e confiabilidade, bastando para isto plotar as colunas E e F em um gráfico tipo linha. Os gráficos podem ser visualizados na Figura 7 abaixo:

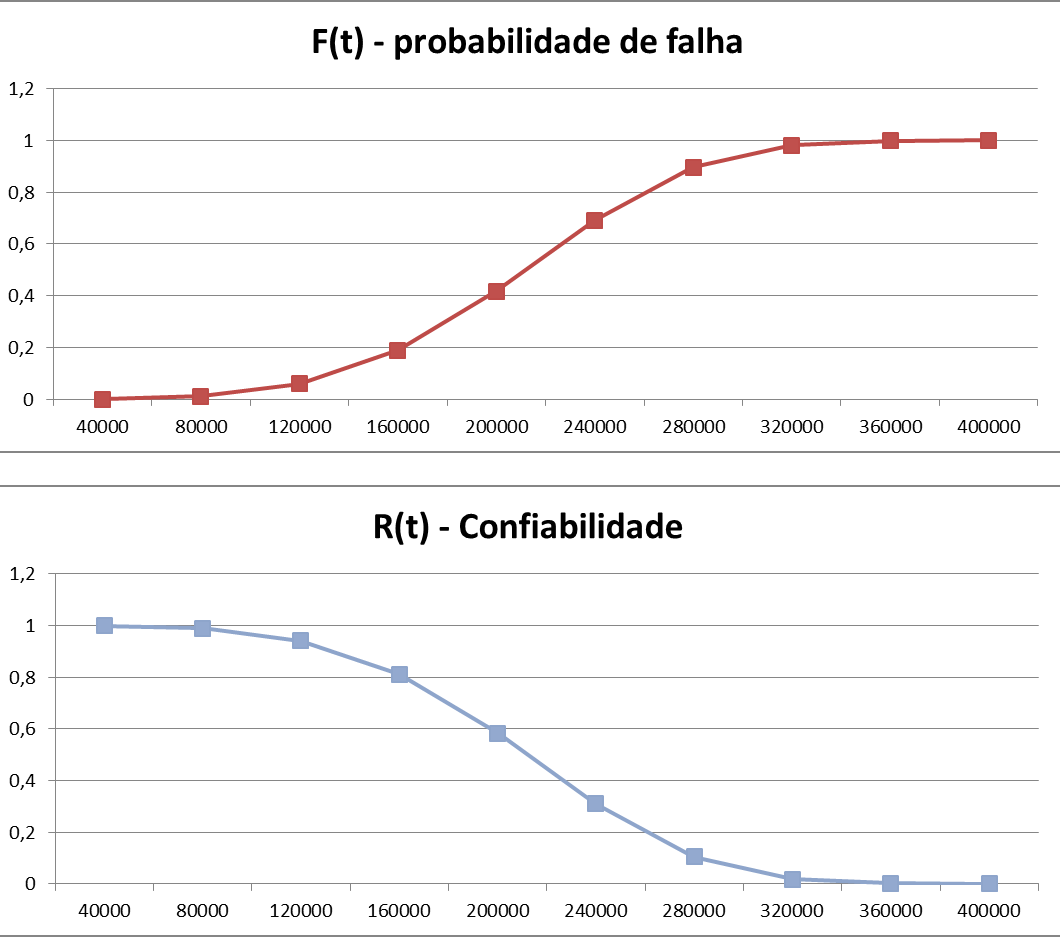
Figura 7 – Gráficos de probabilidade de falha e confiabilidade.

Com as funções e curvas obtidas, é possível associar os custos de manutenção preventiva e manutenção corretiva para obter o custo total de manutenção. Para isto, o primeiro passo é equalizar os custos, calculando-os por unidade de tempo. Assim, é necessário utilizar a seguinte fórmula:

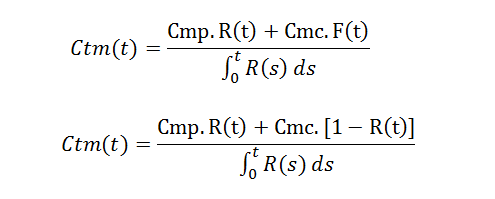
Fórmula para o cálculo do custo total de manutenção considerando as manutenções preventiva e corretiva.

É importante notar que o custo de manutenção preventiva por unidade de tempo é o equivalente ao custo de manutenção preventiva multiplicado pela função confiabilidade R(t) e dividido pela integral da função R(t). Já o custo de manutenção corretiva é calculado de forma similar, bastando substituir a função confiabilidade R(t) pela função F(t) pertinente à probabilidade de falha.

Utilizando a fórmula acima, agora é possível calcular os custos totais de intervenção e determinar o tempo ótimo de manutenção. Para isto, vamos preencher mais uma tabela, conforme o procedimento abaixo:

1. Na mesma planilha utilizada para traçar as curvas de confiabilidade, preencha a partir da célua A15 até A95  os valores de 0 a 400.000 espaçados de 5.000;
2. Na célula B15, insira a fórmula: “=WEIBULL(A15;$B$2;$B$3;VERDADEIRO)” para calcular a função F(t);
3. Na célula C15, insira a fórmula: “=(1-B15)” para calcular a função confiabilidade R(t);
4. A coluna D será utilizada para auxiliar no cálculo da integral de R(t). Para calcular a integral, utilizaremos a regra do trapézio, um algoritmo comum para cálculo de integrais. Para aplicar esta regra, insira na célula D16 a fórmula: “=((A16-A15)*C15+(A16-A15)*(C16-C15)/2).
5. Com a regra do trapézio aplicada, basta calcular a integral de R(t) que é a somatório das pequenas áreas calculadas no passo anterior. Para realizar o somatório, insira na célula E17 a fórmula: “=SOMA($D$16:D17)”.
6. Como temos em mãos os valores das funções e o valor da integral , agora é possível calcular o custo de manutenção preventiva. Basta inserir na célula F17 a seguinte fórmula: “=($B$5*C17)/E17”.
7. Da mesma forma, procedemos com o cálculo de manutenção corretiva, porém agora utilizando a função F(t). Sendo assim, deve ser inserido na célula G17 a seguinte fórmula: “=($B$6*B17)/E17”.
8. Finalmente com ambos os custos de manutenção calculados, basta somar o custo de manutenção preventiva com o de manutenção corretiva para obtermos o custo total. Sendo assim, na célula H17, deverá ser inserido a fórmula: “=(F17+G17)”.

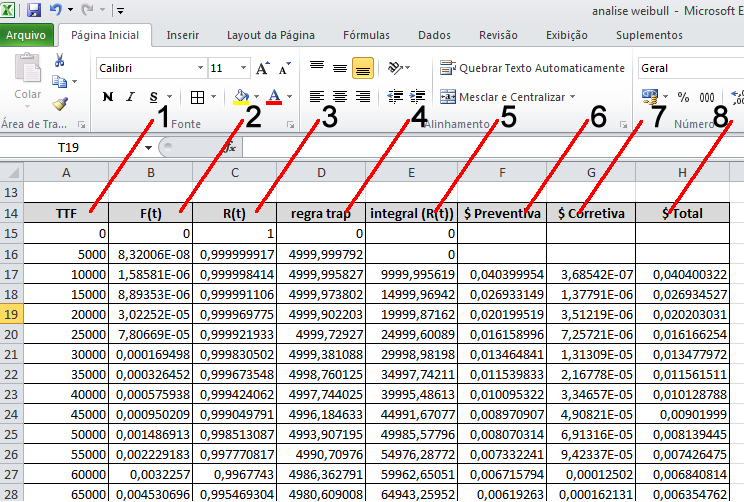
Figura 8 – Tabela com todos os custos de manutenção

Agora que temos todos os valores calculados, basta  plotar em um único gráfico os custos de manutenção preventiva, manutenção corretiva e custo total. O gráfico obtido pode ser visualizado na Figura 9 abaixo.

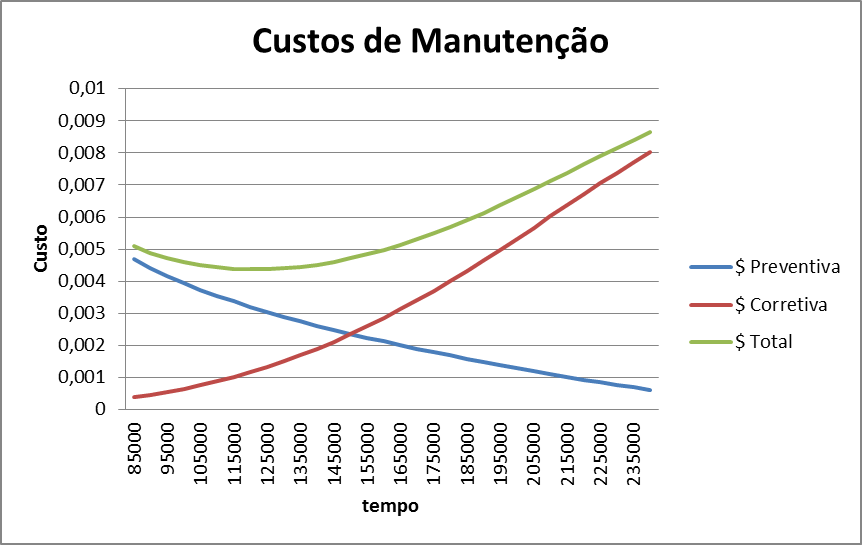
Figura 10 – Detalhe do gráfico da Figura 9

Observe que a curva de custo total possui um ponto mínimo que poderia ser obtido com o cálculo da derivada de sua função. Caso não queira calcular esta derivada, basta achar na coluna H da planilha qual é o menor valor. Isto pode ser feito selecionando o intervalo de custo total e aplicando a fórmula de Mínimo do Excel.

No nosso exemplo, o valor total de custo mínimo por unidade de tempo é R$ 0,00437. Agora basta achar qual é o valor de tempo associado a este custo para determinar o ponto ótimo de manutenção. Para o exemplo, o TTF é 120.000.

Pronto, finalmente encontramos o ponto ótimo de manutenção: exatos 120.000 minutos, ou  2.000 horas, ou 83 dias ou então aproximadamente 2 meses e 23 dias. Pelo nosso cálculo, o ponto ótimo para que seja realizada a manutenção preventiva no cilindro hidráulico é a cada 2 meses e 23 dias. Procedendo desta forma, estaremos adotando a melhor relação custo-benefício de manutenção em um componente que possui os 2 tipos de manutenção, ou seja, manutenção preventiva e corretiva.

Vale destacar que este período encontrado  não garante que o cilindro possuirá manutenções corretivas, pois ainda haverá uma probabilidade de 6% do cilindro hidráulico falhar, o que já é bom. Podemos simular outros custos de manutenção e ver como a determinação do ponto ótimo varia. Se por acaso o custo de manutenção preventiva não fosse R$404,00 e sim R$800,00, o tempo ótimo passaria de 120.000 para 150.000, aumentando o intervalo de manutenção juntamente com a probabilidade de falha que vai para 15%, mas ainda sim obtemos a melhor estratégia. Você poderá simular isto na planilha.

5 – Benefícios da Engenharia de confiabilidade.

Um programa de confiabilidade quando implementado com sucesso é visto como um método para obter vantagem competitiva sobre a concorrência. Pesquisas mundiais indicam que em indústrias de processo diversos, tais como refino e petroquímica, a confiabilidade tem sido utilizada para reduzir os orçamentos de manutenção em até 50%. Uma grande ferramenta utilizada para esta finalidade é o RCM (reliability centered maintenance) que tem o objetivo de analisar as falhas potenciais e definir as melhores estratégias de manutenção (preventiva, inspeção, preditiva, corretiva). Esta ferramenta será objeto de um próximo artigo.

• Redução de perdas de produção com maior operabilidade dos equipamentos;
• Redução do custo unitário de produção devido ao melhor aproveitamento dos ativos;
• Redução dos custos de manutenção;
• Aumento da segurança dos funcionários com a tendência de menor quebra dos equipamentos;
• Melhor estabilidade de processo;
• Melhor aproveitamento da vida útil de componentes e equipamentos;
• Redução do inventário de peças sobressalentes;
• Redução de horas extras;
• Melhoria contínua

6 – Desafios e dificuldades na implantação da confiabilidade

Como relatado no início, este post aborda apenas uma parte da Engenharia de Confiabilidade. Especificamente, com relação à análise matemática, é fácil observar que para obter resultados através de cálculos complexos, é fundamental que haja uma base de dados histórica confiável. A falta desta e alguns outros problemas podem atrapalhar e até mesmo impedir que haja um bom trabalho de confiabilidade na organização. Dentre os diversos desafios a vencer, podemos citar:

• Não apontamento de falhas e motivos de falhas: A falta de apontamento de falhas, motivo e causa das mesmas é um dos principais problemas que atrapalham na análise dos equipamentos. Se não é possível medir, será difícial definir prioridades. É muito importante estruturar uma base de dados confiável e duradoura. Utilizando nosso exemplo, é fácil perceber que para determinar o ponto ótimo do mesmo, partindo-se do princípio que deve haver pelo menos 3 apontamentos, precisamos de uma base sólida de aproximadamente 1 ano. Para estruturar uma boa base de dados, é muito produtivo lançar mão de ferramentas focadas em automação de dados, utlizando sistema de apontamento (Saiba mais sobre este tipo de solução).

• Erros de diagnóstico da operação e de manutentores: Tão ruim quanto não ter base histórica é ter uma apontamento de falhas que não reflete a realidade. Se utilizarmos nosso exemplo do cilindro hidráulico, suponha que ele esteja localizado no braço esquerdo da prensa hidráulica de uma máquina perfiladeira. Se por um acaso a prensa parar por motivo de falha do cilindro, diferentes operadores ou manutentores podem apontar: falha na prensa da perfiladeira, falha no braço da prensa da perfiladeira ou falha no braço esquerdo da prensa da perfiladeira. É fácil perceber que dentre as opções, somente se for apontado a falha no braço esquerdo da prensa da perfiladeira, a informação poderá ser utilizada para a análise da confiabilidade do cilindro. Na maioria das vezes o apontamento não é realizado de forma correta e atrapalha toda a análise futura. Um outro exemplo poderia ser uma contaminação no óleo hidráulico que provoca a falha do cilindro hidráulico. Ao realizar o reparo, o manutentor pode deixar de verificar a qualidade do óleo e constatar erroneamente que a falha foi do cilindro quando na verdade a causa raiz que deveria ser apontada seria a contaminação do óleo.

• Falta de informações e documentação histórica de manutenção: Geralmente, após realizar a manutenção, o equipamento que sofre manutenção, as horas gastas, a quantidade de recursos humanos e os materiais utilizados, bem como a descrição das atividades devem ser registradas em um documento, normalmente denominado ordem de manutenção. Um problema que ocorre frequentemente é a falta de apontamento destas infomações. Isto dificulta bastante uma análise profunda do histórico de custos e recursos necessários para o cálculos dos custos de manutenção corretiva e preventiva. Além disto, fica difícil estimar o tempo de atendimento para determinada falha.

Os estudos de Confiabilidade são muito importantes, porém mais importante ainda é trabalhar na confiabilidade da base do sistema. Deve-se ter uma rotina muito bem estabelecida com uma programação de manutenção adequada, utilização correta de documentos e equipe qualificada para realizar diagnósticos. Somente desta forma será possível aplicar cálculos complexos buscando a melhoria contínua. Com uma base bem fundamentada e informações sólidas, os estudos de confiabilidade proporcionam ganhos enormes para a organização e consequentemente aumentam sua competividade perante o mercado. 

 7 – Anexo: Como configurar o Excel para utilizar a ferramenta de análise

1. Clique no menu Arquivo – Opções;
2. Clique em Suplementos;
3. Na parte de Suplementos do Excel, clique em ir…

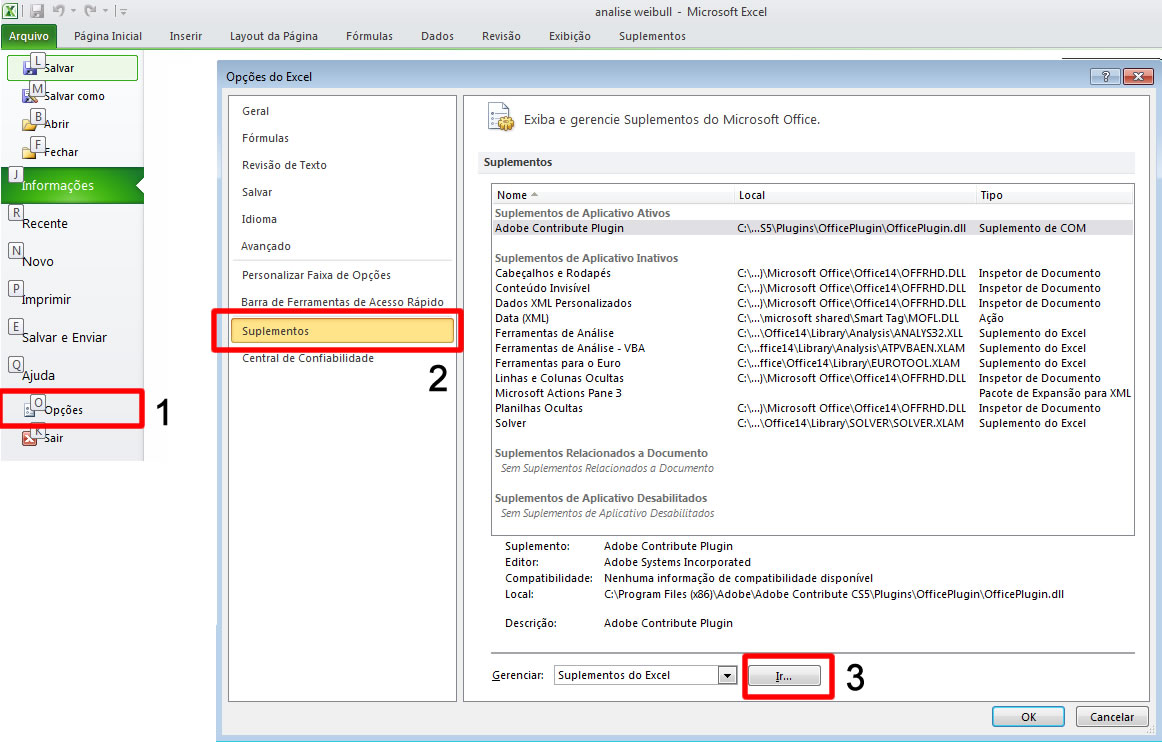
configurar excel ferramentas analise

A janela de de suplementos será aberta. Então proceda da seguinte forma:

1. Habilite a caixa Ferramentas de Análise
2. Clique no botão Ok
3. Após seguir estes procedimentos a opção Análise de Dados será habilitada. Para checar, basta clicar no menu Dados e verificar no canto direito da tela, como indica o passo 3 da figura abaixo.

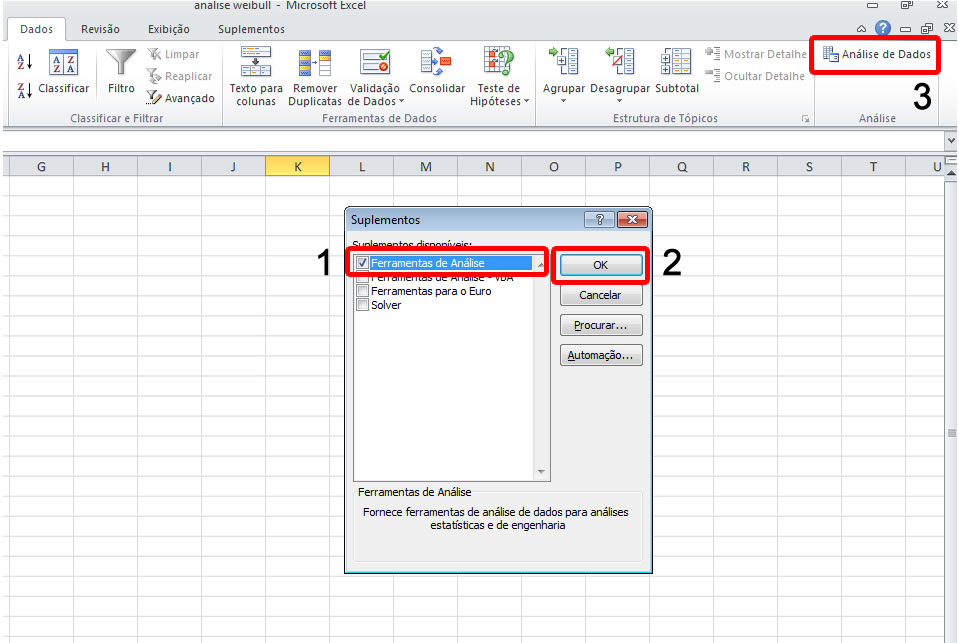
configurar excel ferramentas analise2

Pronto, agora o excel está configurado para utilizar as ferramentas de análise.